Newton
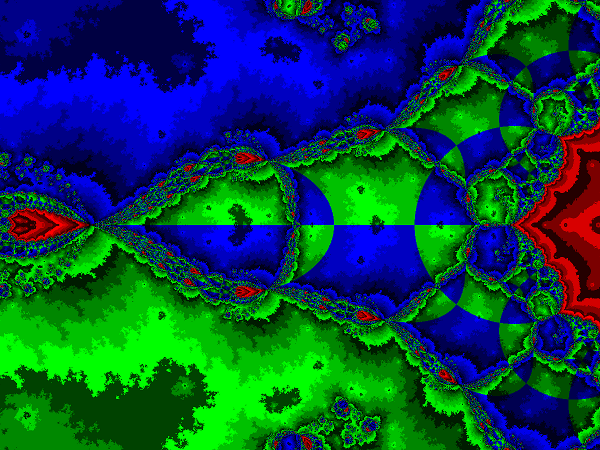 Newton-Fraktal für z4-log2(z)-2, Ausschnitt
[-1.2,1.2] × i[-0.9,0.9]
Newton-Fraktal für z4-log2(z)-2, Ausschnitt
[-1.2,1.2] × i[-0.9,0.9]
^4+1)*z*z*z+1_1248535776.png) Newton-Fraktal für z15+z3+1, Ausschnitt
[-1.2,1.2] × i[-0.9,0.9]
Newton-Fraktal für z15+z3+1, Ausschnitt
[-1.2,1.2] × i[-0.9,0.9]
 Newton-Fraktal für z3-1, Ausschnitt
[-1,1] × i[-1,1]
Newton-Fraktal für z3-1, Ausschnitt
[-1,1] × i[-1,1]
License: GPL v2
Download: newton-0.3.tar.gz (229,4 KB)
Inhalt
Voraussetzung für den Betrieb dieses Programms ist
das GIMP Toolkit GTK+-2.
Kompilieren mit make.
Es stehen mal wieder Klausuren an, also war es höchste Zeit, endlich ein neues Programm zu schreiben.
Das Programm berechnet für in die komplexe Ebene (linear) gemappte Pixelkoordinaten als Startwerte z0 für das Newton-Verfahren
zk+1 = zk - f'(zk)-1 · f(zk)
die Nullstellen einer angegebenen Funktion. Den Nullstellen werden unterschiedliche Farben zugewiesen und die Iterationszahl wird in die Helligkeit der Farbe des Pixels umgesetzt. Dadurch entstehen Fraktale wie die Abgebildeten.
Beschreibung
Mit newton war ich erstmals in der Lage, sinnvoll einen
Recursive Descent Parser einzusetzen,
um die Formeln zu parsen. Die drei Bilder wurden erstellt mit den Befehlen
newton -f 'z^4-log(z)^2-2' '4*z^3-1/z' -1.2,1.2 -0.9,0.9 1200newton -f 'z^15+z^3+1' '15*z^14+3*z^2' -1.2,1.2 -0.9,0.9 1200newton -f 'z^3-1' '3*z^2' 1200
Wie man oben sieht, kann das Programm selbst (noch?) nicht analytisch differenzieren, sodass die Ableitung der Funktion ebenfalls benötigt wird. Ebenfalls in der Planung aber noch nicht vollständig implementiert ist die Reduktion und Optimierung der Formel zur schnelleren Berechnung.
Die Berechnungen für ein gegebenes z, das eine auf die komplexe Ebene gemappte Pixel-Koordinate ist, erfolgt über die in umgekehrte Polnische Notation überführte Formel in Linearzeit, exklusive der eventueller Funktionsaufrufe, wie z.B. für zb oder z!.
Den Parser für die Formeln habe ich versucht, erweiterbar und generisch zu halten, zumindest soweit es
hier sinnvoll ist. So erlaubt er eine Übergabe von zu erkennenden Funktionsnamen wie sin,
abs oder auch gamma
sowie eine weitere Liste von Variablen, hier u.a. benutzt: z,
i, pi, wobei letztere
beiden natürlich Konstanten sind, die bei der Minimierung (siehe nächsten Abschnitt) als solche behandelt
werden und während der Berechnung nicht mehr explizit auftauchen.
Der erstellte Baum wird vor der eigentlichen Berechnung der Breite*Höhe Pixel noch rudimentär versucht zu minimieren, indem konstante Ausdrücke vorausgewertet werden. Allerdings ist weder Assoziativität noch Kommutativität (über Baum-Rotationen) implementiert, sodass zwar bspw. x+1+1+1 = x+(1+(1+1)) zu x+3 aber nicht 1+1+1+x = 1+(1+(1+x)) minimiert werden können.
Die Graphikausgabe erfolgt über die libSDL und ich arbeite momentan noch an einer interaktiven Zoomfunktion sowie der Möglichkeit, den dargestellten Ausschnitt zu verschieben. Durch Drücken der Taste 'h' im Graphikmodus wird in der Konsole eine Übersicht über die Funktionen ausgebenen, so existiert eine Möglichkeit das gerenderte Bild zu speichern und später werden noch andere Kommandos unterstützt werden. ESC oder 'q' beenden das Programm.
Zusätzlich zum Bild werden mit dem Switch -v noch die gefundenen, auf maximal 16
Stellen
genau approximierten (da dies der Genauigkeit des intern durchweg benutzten Datentyps
double
complex entspricht) Nullstellen der
Funktion in der Konsole ausgegeben.
Changelog
- 02.10.2009: Release v0.3:
- Dialog zur Auswahl der Farben für die verschiedenen Nullstellen der gerenderten Funktion hinzugefügt
- Neuberechnung des Bildes aus den Iterationsergebnissen in separaten Thread verlagert -> verzögerungsfreieres Updaten (bspw. der Farben des Bildes)
- Bedienungserleichterung durch Shortcuts für einige Funktionen hinzugefügt
- Beschleunigung des Renderns durch:
- Entfernung einiger durch die neue GTK+-GUI unnötig gewordener, wiederholter Abfragen
- Threading: es werden standardmäßig alle verfügbaren (auch
virtuellen) Prozessoren zur Berechnung genutzt ->
Geschwindigkeitssteigerung insbesondere auf Mehrkernprozessoren. Die Anzahl benutzter Threads ist optional mit dem
Parameter
-teinstellbar - Optimierung der Suche nach den zu den Berechnungsergebnissen passenden Nullstellen von O(n) zu O(log n)
- Berechnung mehrerer Pixelwerte in einem Evaluierungsschritt, siehe unten
- Übersetzung des restlichen Programms ins Deutsche abgeschlossen
- Mehrere Fehlerausgaben und -Überprüfungen für Benutzereingaben hinzugefügt
- Zoomen mit Maus: Rechtsklick zoomt heraus, mit der linken Maustaste lässt sich das zu vergrößernde Rechteck wählen, Shift deaktiviert das Erhalten des Seitenverhältnisses für die Selektion
- Die Farben der Nullstellen bleiben beim Zoomen gleich (gilt noch nicht für selbstgewählte Farben)
- Speicherbedarf für die Zwischenwerte beim Rendern auf feste 4 Byte pro Pixel reduziert (vorher bei x86: 8, x64: 12)
- Das Makro
PACKdefiniert zur Compile-Zeit, wieviele Pixelwerte pro Rechenschritt verarbeitet werden. V.a. für kurze Formeln steigert hier eine hohe Zahl den Durchsatz bis auf das Doppelte, während er für längere Formeln absinkt. Voreingestellt sind 2 Pixel/Rechenschritt - Das Makro
VAL_Tdefiniert, ob als Datentyp zur Berechnungfloat(32 Bit, keine nennenswerte Geschwindigkeitssteigerung),double(64 Bit, Standard) oderlong double(80 Bit, langsam) verwendet wird
- 10.09.2009: Release v0.2
- GTK+-Interface hinzugefügt
- Start mit
./newtonmöglich, ohne Formel oder andere Parameter initial angeben zu müssen - Übersetzung ins Deutsche (GUI vollständig, Rest teilweise) mittels GNU gettext
- Sechs Formeln als Voreinstellung inklusive Vorschaubild in GUI selektierbar
- Einbau eines
errno-Mechanismus in den Formelparser
- 04.08.2009: Release v0.1.1
- GUI-Code ausgegliedert
- Durch Optimierung des Berechnungscodes läuft das Programm jetzt ungefähr doppelt so schnell
- Vorbereitungen zum Kompilieren der Formel
- Ersetzung der
cpow-Funktion der glibc durch die (inline-bare) BSD-Variante (diese hat nach meinen Tests auch konstante Laufzeit für beliebige Exponenten, sodass die unten beschriebenen Tricks nicht mehr nötig sind) - Speicherreduktion und Geschwindigkeitssteigerung durch Umbau des internen Datentypen zur Speicherung der Iterationsergebnisse
- 27.07.2009: Release v0.1
What's next?
- Implementierung der Assoziativität und Kommutativität der Operatoren zwecks Reduktion der Formel
- Automatische Umschreibung der Formeln, sodass doppelte Berechnungen innerhalb einer Formel gespart werden können: ersetze bspw. z3+z5 durch z3·(1+z2)
- Ersetze gleiche Teilausdrücke in Formeln für die Funktion und die Ableitung, sodass doppelte Berechnungen innerhalb beider Formeln gespart werden können, bspw. statt f(z) = z3-1 und f'(z) = 3·z2 definiere t = z2 und benutze f(z) = t·z-1 sowie f'(z) = 3·t, wobei t lediglich einmal pro Iteration berechnet werden muss
- Kompilierung der Formel in Maschinencode; dadurch können (alle!) bedingten Sprünge während der Berechnung vermieden werden
- Möglichkeit der Nutzung der Graphikhardware zur Berechnung mehrerer Pixel gleichzeitig (→ Genauigkeit?)
- Funktion, die schönere Farbabstufungen liefert
- Verschieben des gezeigten Ausschnitts via mittlerer Maustaste
- Darstellung des bereits berechneten Ausschnitts während der Berechnung
Geschwindigkeit
| CPU | GCC- Version |
z·z·z-1 Details: #1 |
z·z·z·(1+z12)+1 Details: #2 |
|
|---|---|---|---|---|
| Typ | Taktung | |||
| Pentium 4 | 1,6 GHz | 4.2.3 | 194k px/s | 25k px/s |
| 4.3.3 | 201k px/s | 26k px/s | ||
| Pentium-M | 2 GHz | 4.2.4 | 465k px/s | 63k px/s |
| 4.3.3 | 473k px/s | 66k px/s | ||
| 4.4.1(a) | 464k px/s | 65k px/s | ||
| Athlon XP-M | 2,3 GHz | 4.3.3 | 480k px/s | 65k px/s |
| Core 2 | 3 GHz | 4.2.4 | 960k px/s | 118k px/s |
#1 Aufruf: newton -f 'z*z*z-1' '3*z*z' -v 2000 -b,
maximal 56 Iterationen.
#2 Aufruf: newton -f 'z*z*z*(1+z^12)+1' 'z*z*(3+15*z^12)' 1000 -v -b,
maximal 200 Iterationen.
(a) es wird das seit GCC 4.4
optional verfügbare Graphite-Framework basierend auf
PPL zur
Schleifen-Optimierung
genutzt.
Dieser Absatz gilt nur für Version 0.1 und ist deshalb bloß als Notiz an mich selbst von Nutzen
Die am Anfang angegebenen Formeln werden recht langsam berechnet, weil für kleinere
b die Berechnung von
ab durch die in der Standard-Library enthaltene Funktion
cpow(a, b) mehr Aufwand erfordert als das b-fache
Hintereinander-Multiplizieren von a. Selbstverständlich ist diese Vorgehensweise
nur bei natürlich-zahligen Exponenten möglich. Bei meinen Tests habe ich festgestellt, dass
zb mit einem Pentium-M, GCC 4.2.4 und glibc 2.10.1 unter Linux erst ab
b > 11 schneller durch cpow berechnet wird. Es empfiehlt sich also,
z3 als z·z·z und auch
z15+z3 als
z·z·z·(1+(z·z·z)4) zu
schreiben. Selbes gilt bei der Ableitung.
Aufruf
[-e ] [-i ] [[ ],[ ] [ , ]] [ [ ]] The formula may contain the usual operators: +,-,*,/,^,! and groupings in parantheses. The variables are interpreted in the complex plane, whereas z = x + i*y; others than x,y,z are not allowed. Additionally the following constants may be used: pi = 3.14159+0i Pi e = 2.71828+0i Euler's number e i = 0+1i Imaginary unit i The following functions are supported (r: real, c: complex): [ c] conj Complex conjugate [ c] re Real part of the complex value [ c] im Imaginary part of the complex value [rc] abs Absolute value / Norm / Modulus [ c] arg Argument / Angle of the complex value [rc] sin Sine [rc] arcsin Arcsine [rc] cos Cosine [rc] arccos Arccosine [rc] tan Tangent [rc] arctan Arctangent [rc] exp Exponential function [rc] log Natural logarithm [rc] sqrt Square root [rc] gamma Factorial / Gamma function [rc] lgamma Logarithm of the gamma function Arguments: -f sets the function f(z) for which the Newton-Iterations will be calculated. Remember to escape any symbols that may be interpre- ted by your shell. -e maximal difference between two calculated values to consider them equal; format is a formula without any vars, default is 1e-14 -i maximal number of iterations to perform, default is 200 -F fullscreen mode (toggle via 'f' when the application runs) -b enable benchmark mode: no graphics are generated, just the plain calculations are performed -s print out some statistics about the iterations -v be more verbose, use twice for greater effect]]>
Siehe auch: Eine Erläuterung der üblichen Parameterangabesyntax.
Funktionsweise
Für einen Pixel (x,y) aus dem zu rendernden Bildbereich (x=0,…,width-1 und y=0,…,height-1) wird der Punkt z = Re(z) + i·Im(z) in der betrachteten Fläche [a,b] × i[c,d] der komplexen Ebene bestimmt durch
Re(z) = a + (b-a)·x/(width-1)
Im(z) = c + (d-c)·y/(height-1)
Zu beachten ist hier, dass die Pixelkoordinaten ihren Ursprung gängigerweise oben links im Bild haben, die y-Koordinate also negiert zu Im(z) ist und das Bild an der Horizontalen gespiegelt gerendert wird.
Der kritische Teil des Programms ist eindeutig die Berechnungsfunktion für die Formel. Pro Iterationsschritt muss er einmal für f(zk) und ein weiteres Mal für f'(zk) ausgeführt werden. Anhand der Formeln f(z) = z3-z/4 und f'(z) = 3·z2-1/4 möchte ich zur Veranschaulichung die Arbeitsweise des Programms durchspielen.
Aufruf: newton -f 'z*z*z-z/4' '3*z*z-1/4'
Nach dem Parsen der Formeln liegen f und f' (vereinfacht*) in folgender Baumrepräsentation vor:
*: Tatsächlich behandelt der Formelparser den Operator "-" und den darauf folgenden Ausdruck als Sonderfall (nämlich als inverses Element des Ausdrucks bezüglich der Addition) und ersetzt bspw. a-b+c durch a+(0-b)+c.
Dies vereinfacht die Definition der formalen Grammatik zur Beschreibung von mathematischen Formeln, die dem Parser zugrunde liegt. Deshalb sind die Abbildungen nicht ganz korrekt, aber der Einfachheit halber wird auf diese Feinheit verzichtet.
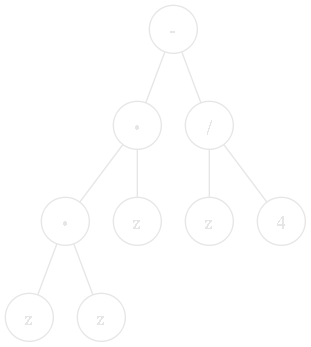 f
f
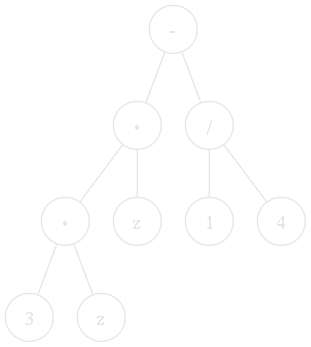 f'
f'
Nach Zusammenfassung des konstanten Ausdrucks 1/4 zu 0.25 in der Ableitung werden die beiden Bäume in je einen Stack in umgekehrter polnischer Notation überführt:
- f:
z z * z * z 4 / - - f':
3 z * z * (0.25) -
Dieser Stack bietet nun die Möglichkeit einer effizienten Berechnung der Formel für beliebig einzusetzende z. Ausgehend von links wird jedes Element betrachtet, eine entsprechende Aktion durchgeführt und der Stack möglicherweise verändert. Selbstverständlich arbeitet man auf einer Kopie des Stacks, sodass die ursprüngliche (obige) Form für weitere Berechnungen erhalten bleibt.
| 1 | z z * z * z 4 / - |
| 2 | 4 z * z * z 4 / - |
| 3 | 4 z * z * z 4 / - |
| 4 | 4 4 * z * z 4 / - |
| 5 | 4 4 * z * z 4 / - |
| 6 | 16 z * z 4 / - |
| 7 | 16 z * z 4 / - |
| 8 | 16 4 * z 4 / - |
| 9 | 16 4 * z 4 / - |
| 10 | 64 z 4 / - |
| 11 | 64 z 4 / - |
| 12 | 64 4 4 / - |
| 13 | 64 4 4 / - |
| 14 | 64 4 4 / - |
| 15 | 64 1 - |
| 16 | 64 1 - |
| 17 | 63 |
Die genannten Aktionen beschränken sich im im Wesentlichen auf die Ausführung der arithmetischen Operationen auf den (ein oder zwei, je nach Stelligkeit des Operators) vorangehenden Elementen des Stacks. Das Ergebnis der Operation wird im am weitesten links stehenden Operanden bzw. Stackelement gespeichert und dieses im nächsten Schritt als Vorangehendes des nächsten Elements gesetzt, sodass sowohl das Operatorelement als auch (im Fall eines zweistelligen Operators) dessen vorangehendes Element aus dem Stack gelöscht werden. Zusätzlich wird, falls das aktuelle Stackelement eine Variable repräsentiert, diese durch den fixen Wert ersetzt, für den die Formel zu berechnen ist. Hier wird je ein zu einem Pixel gehöriges z (siehe Kasten Mapping) eingesetzt.
Genauer werden folgende Aktionen auf dem Stack für ein aktuelles Element durchgeführt:
- Variable:
a = pop; b = Wert[a]; push b;- Fester Wert:
a = pop; push a;- 1-stellige Operatoren (Funktionsaufruf, !):
op = pop; a = pop; b = op(a); push b;- 2-stellige Operatoren (^, *, /, +, -):
op = pop; b = pop; a = pop; c = op(a, b); push c;
Wie im Beispiel zur Berechnung von f(4) erkennbar ist, werden allein für das Abarbeiten des Stacks dieser einfachen Formel (und mit dieser Zählweise) 17 Arbeitsschritte benötigt. Darin enthalten sind nicht die nötigen (Rechen-)Schritte, die eine Operatorauswertung erfordert. Dies erklärt, warum die Berechnung den kritischen Teil des Programms ausmacht.
**: In der Tat wäre der Versuch interessant, die Ersetzung erst bei Variablenzugriff durch andere Operationen auszuführen und nicht schon bei Erreichen eines Variablenelements, um mehrfaches Ersetzen und damit überflüssiges Kopieren von Speicherinhalten zu sparen. In vielen Formeln machen Variablen den Großteil der Elemente aus.
Da der Compiler für die Auswertung der Operatoren *, /, + und - bereits optimierten Maschinencode erzeugt und die anderen Operationen kaum weiter zu beschleunigen sind, da sie entweder trivial (Variablenersetzung**, fester Wert) oder bereits ausreichend studiert (Fakultät, Potenzierung) sind, kann hier lediglich die Abarbeitung des Stacks optimiert werden. Dazu zählt vor allem die Entscheidung, was mit dem aktuellen Stackelement geschehen soll bzw. das Erkennen, um welche Art von Stackelement es sich handelt.
Zwei mögliche Herangehensweisen an dieses Problem möchte ich im Folgenden vorstellen.
Überprüfung
Für die Überprüfung um welche Art von Element es sich handelt zur Laufzeit (im Gegensatz zur Compile-Zeit) bieten sich zwei (leicht) verschiedene Lösungswege an.
switch
Zur Entscheidung, um welchen Typ es sich bei einem Element handelt, enthalten die Stackelemente einen Identifikationswert, der überprüft werden kann. Der Code zum Abarbeiten des Stacks sieht im Prinzip wie folgt aus:
for (next elem in stack) do switch (elem.id) case Variable: a = pop; b = Wert[a]; push b; break; case Wert: a = pop; push a; break; case Op1: op = pop; a = pop; b = op(a); push b; break; case Op2: op = pop; b = pop; a = pop; c = op(a, b); push c; break; end end
Offensichtlich werden hier die Überprüfungen für ein Stackelement bei allen Berechnungen der Formel immer dasselbe Ergebnis liefern, d.h. eine Variable bleibt immer eine Variable und muss ersetzt werden, genauso verhält es sich mit den anderen Typen. Dies bedeutet bei der Berechnung einen Mehraufwand, der insofern unnötig ist, als die Auswertung, welche Aktionen in welcher Reihenfolge ausgeführt werden müssen, im Prinzip schon nach dem Parsen der Formel feststehen und nicht in jeder Abarbeitung des Stacks neu ermittelt werden müssten.
Funktionszeiger
Weise jedem Stackelement statt eines Identifikationswertes eine (kleine) Funktion zu, die für dieses
Element aufgerufen wird und für dieses Element die entsprechende (oben aufgeführte) Aktion durchführt. Da
newton in der nicht-Objekt-orientierten Sprache C geschrieben wurde, "weiß" die Funktion nicht,
zu welchem Stackelement sie gehört, also wird ihr das über einen Parameter mitgeteilt.
Der entsprechende Code wäre dann:
for (next elem in stack) do elem.func(elem); end
Diesmal nicht so offensichtlich wie oben, versteckt sich auch hier nahezu derselbe Mehraufwand, der sich indes erst klar zu erkennen gibt, wenn man sich den zugehörigen Maschinencode ansieht. In dem Moment, in dem der Prozessor zur Ausführung des Schleifenrumpfes kommt, ist bekannt, dass die nächste(n) Instruktion(en) einen Funktionsaufruf ausführen. Allerdings ist zu diesem Zeitpunkt noch nicht bekannt, um welche Funktion es sich handelt, denn diese Information liegt nicht im Maschinencode vor (die Funktion ändert sich mit jeder anderen Formel, die eingegeben wird, der Compiler "kennt" sie nicht), sondern nur im Speicher. Im Gegensatz zu einem im Vornherein bekannten Ziel, dauert die Evaluation einer solchen Speicheradresse und der Sprung zu einem im Voraus unbekannten Ziel deutlich länger. Solange das Sprungziel nicht bekannt ist, kann der Prozessor parallel zur Ausführung des aktuellen Befehls noch nicht die nächste Instruktion laden und dekodieren. Dies resultiert in der angesprochenen Verzögerung.
Zugegebenermaßen sind aktuelle Prozessoren inzwischen bei dieser Auswertung sehr schnell (bzw. können das Sprungziel
im Cache halten), sodass diese Methode mit Funktionszeigern etwas schneller läuft, als die Methode mit der
switch-Anweisung. Dennoch bleibt die Auswertung mit demselben Argument wie oben unnötig und könnte im
Prinzip vermieden werden.
Die Methode der Funktionszeigerzuweisung an Stackelemente wird momentan benutzt.